Chapter 21 Deep Learning

Introduction

• 圖片展示

  

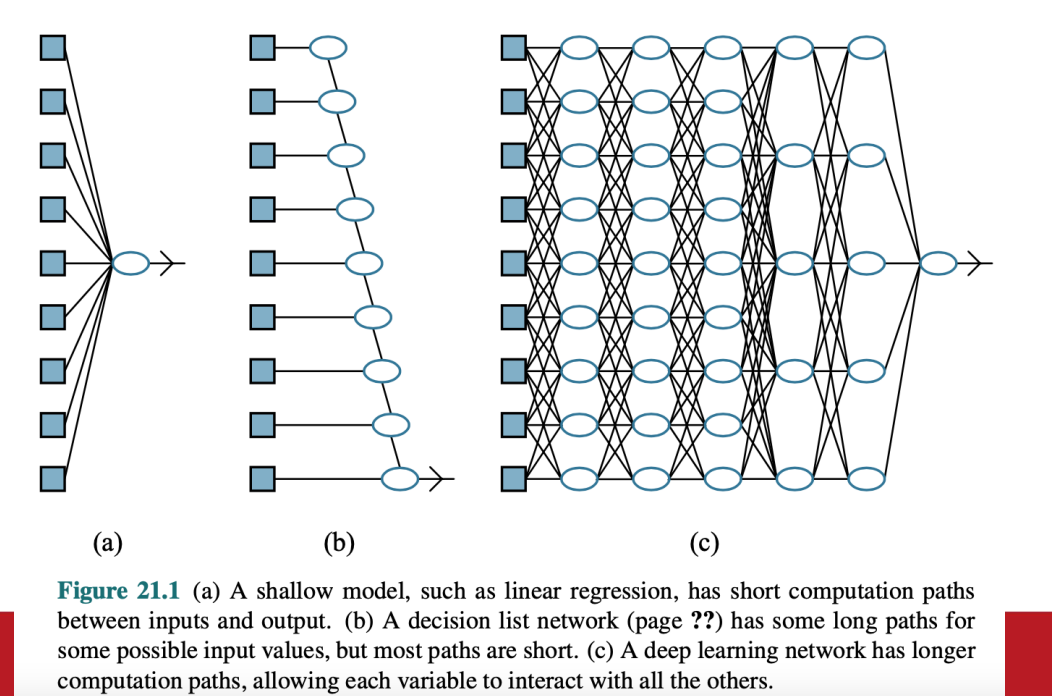
Simple Feedforward Networks

• 只有單向連結的網路

  

  • feedforward
  • input: 網路的參數

Networks as complex functions

• 應用非線性的函數得到輸出

  

  • 寫成 vector form

• 非線性的啟動函數

  

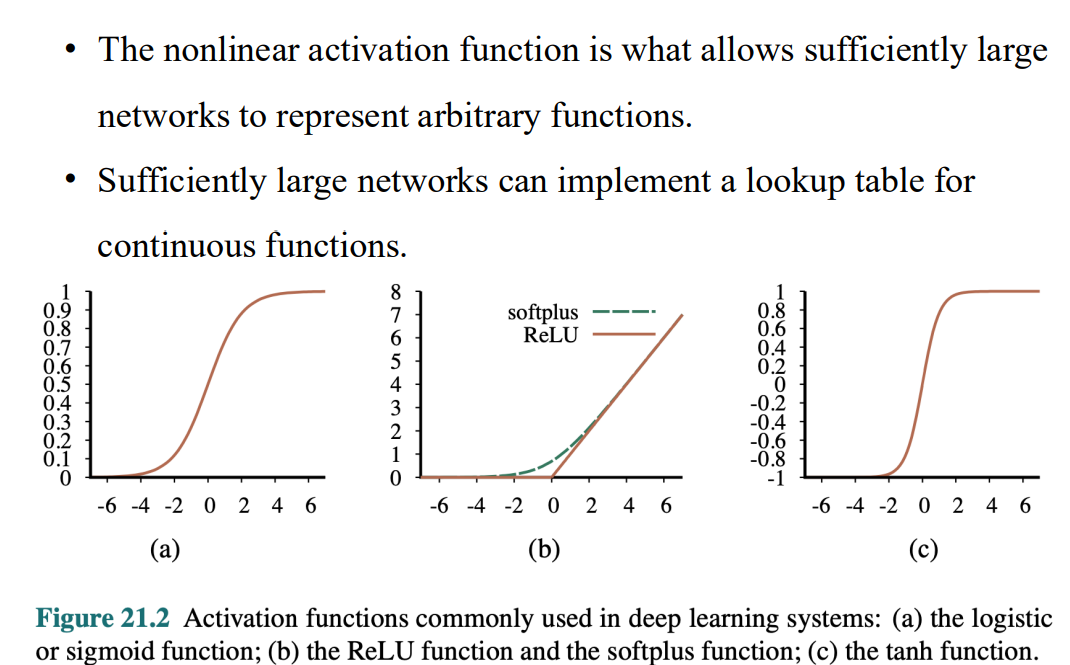
  • 理論上 神經網路夠大 非線性函數可以逼近任何函數

• network

  

  • 激活函數的導數 都是非負的

    

  • 上圖的拆解

    

  • fully connected: 上一層的每個點 都有連接到下一層的每個點

Gradients and learning

• loss function

  

  • 沿著損失函數的梯度方向走

    

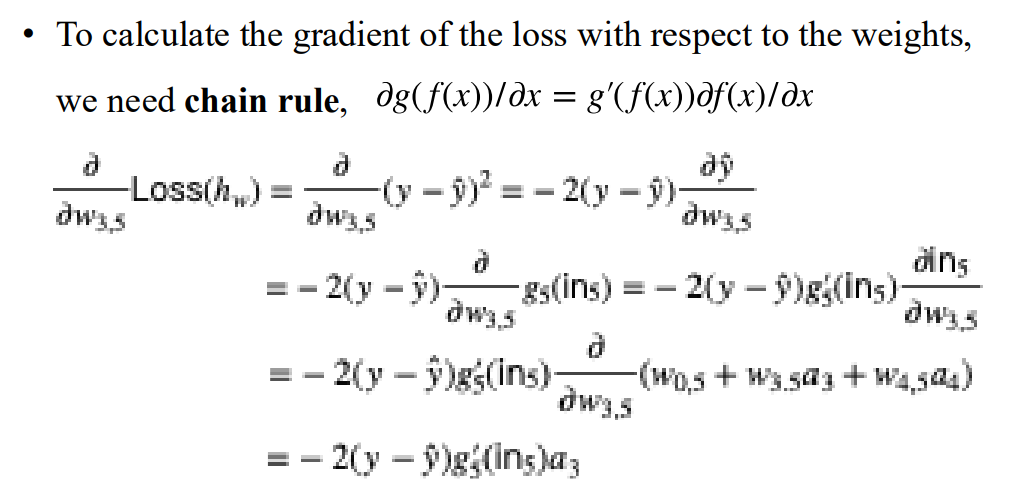
  • by chain rule

    

  • 針對複雜的權重 可能要做到多次的chain rule

• 以 的梯度作為例子

  

  • 被稱之為 perceive error

    

  • 如果很大 則可能並不重要 因此不需要改變
  • 則是一種反向傳播的例子 因為他是 乘上從5回到3的路徑 (back propagation)

• 梯度消失

  

  • 如果局部導數很小 或接近於0 => 改變權重對於輸出的影響極小

Computation Graphs for Deep Learning

• 輸入與輸出

  

• 評估與gt的差距函數 輸出層

  

  • 對於N個sample 使用negative log likelihood
  • 對於分佈 使用cross entropy loss
  • 實務上 我們不知道P的真實分佈 所以得估計

    

  • 對於布林輸出 使用sigmoid outputlayer
  • 對於多類別分類 使用softmax layer

    

  • 對於回歸問題 使用linear layer
  • 更多輸出層都是可能的 例如mixture density

Hidden layers

• 每層的數值只是輸入的不同形式

  

  • 輸入到輸出複雜的轉換 透過多個層來解離 變成簡單的轉換 更容易透過local updating process學習

Convolutional Networks

• 簡化計算 讓每個隱藏層的單元 只需要處理部分區域的圖片

  

• 空間不變性

  

  • 圖像中相同的特徵 都應該被以相同的方式被網路檢測到
  • unit in hidden layer 會使用相同的權重計算 實現一致性

• 名次定義

  

  • CNN
  • convolution
  • kernal

• 捲積操作範例

  

  • kernal dot product 對應的x向量

    

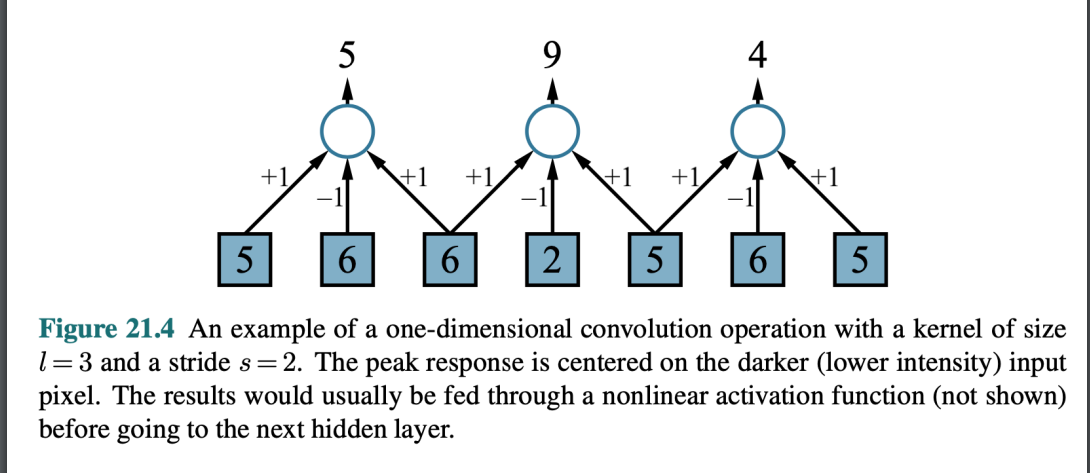
  • 圖例

• stride

  

• receptive field

  

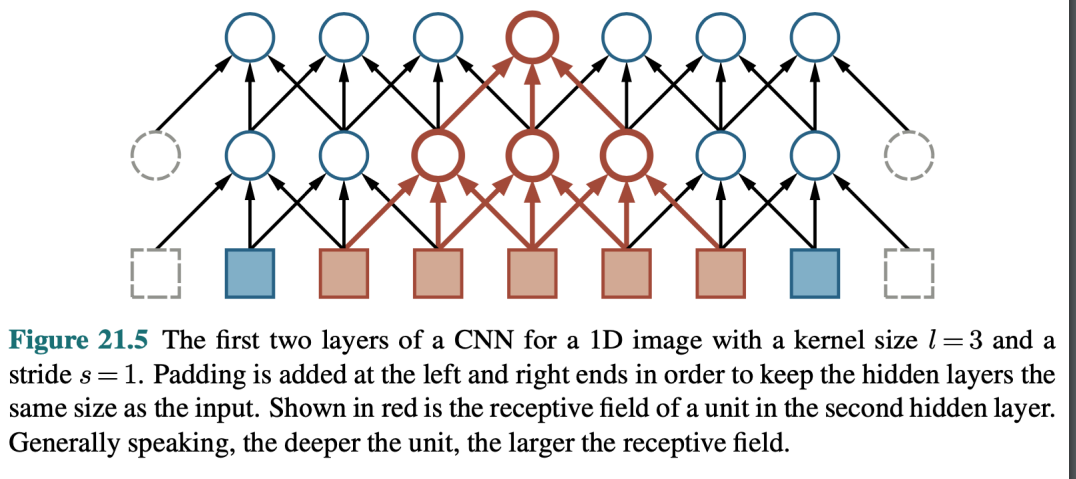
  • 越深的層 感受野越大
  • padding 範例

• 卷積操作可以看成 matrix multiplication

  

• 因為有k個kernal 維度會增加1

  

• CNN

  

Pooling and downsampling

• two type of pooling

  

  • 平均池化
  • 最大池化
  • 池化層的作用：
    • 在卷積神經網絡（CNN）中，池化層的主要功能是對局部區域的輸出進行壓縮或總結，以減少數據的尺寸（downsampling）。
    • 它的輸入通常來自卷積層的特徵圖，目的是提取重要信息，同時丟棄不必要的細節，從而降低計算成本並提高網絡的泛化能力。